Our software rectifies shortcomings of phenomenological-based models for a highly accurate description and prediction based on our real data-generating process.
The only input these models require are the nominal structural design (layer width, material compositions and possible doping concentrations) and well-known basic material parameters that can be found in the standard literature, like bulk bandstructure parameters (Luttinger parameters, strain constants and bandgaps), lattice constants, phonon coupling constants, background refractive indices, dielectric constants and band-offsets.
They do not require or allow any phenomenological fit parameters like line broadenings, dephasing times or radiative- or Auger-recombination constants. They have been tested for various materials and device configuration to yield quantitatively correct results within the scattering of the experiment (see the examples). Thus, they are truly predictive.
For all calculations we use fully coupled 8×8 kp-bandstructure models (see Refs.[10], [31]). For dillute Nitrides this is coupled to an anti-crossing model for the conduction bands (see Ref.[8]).
If internal electric fields due to piezoelectric effects or ionized dopants or external electric fields due to applied Voltages are present, the screening of these fields by charge inhomogenities is included by coupling the bandstructure calculation self consistently to a Poisson solver.
Although not required by the models, Gain Tables generally assume that the carriers are in thermal equilibrium and can be described by Fermi distribution. Non-equilibrium effects like carrier relaxation and spectral hole burning and their influence on spectral properties can be investigated in a consulting type environment.
Details about the theoretical models can be found in the SimuLase manual and our various publications.
The typical use of SimuLase™ and data created by it is described for the examples of an edge emitting device and a VECSEL in the examples guide.
The gain/absorption and carrier-induced refractive index changes are calculated by solving the semiconductor-Bloch equations, i.e. the equations of motion for the microscopic optical polarizations. Here, incoherent processes, electron-electron and electron-phonon scattering, are treated explicitly by solving the corresponding quantum-Boltzmann type scattering equations in second Born-Markov approximation. As demonstrated here, this is not only necessary for correct line shapes, but also for amplitudes and spectral positions. In these calculations we also include the Coulomb induced inter subband coupling and the conduction band nonparabolicity.
The spontaneous emission and the corresponding radiative carrier lifetime are calculated using the semiconductor luminescence equations. These are the microscopic equations of motion for the photon-assisted polarizations and distribution functions. As for the gain calculations, they involve the solution of quantum-Boltzmann type scattering equations for electron-electron and electron-phonon collisions. They also involve the numerically expensive determination of excitonic correlations.
The shortcomings of the often used, numerically much simpler Kubo-Martin-Schwinger method (a simple integral conversion of absorption/gain spectra into spontaneous emission spectra) are demonstrated here.
For more details about this approach see e.g. Ref.[28] or M. Kira, F. Jahnke, W. Hoyer, S.W. Koch, Prog. Quantum Electron. 23, 189 (1999).
The calculation of carrier recombination’s due to Auger processes and the inverse process, carrier generation due to impact ionization, requires one to solve complex quantum-Boltzmann type scattering processes in the second Born-Markov approximation. The general equations that have to be solved have been known for decades. However, mostly due to numerical limitations, previous attempts to solve them have applied uncontrolled approximations for the involved (Coulomb) coupling matrix elements, spin-, k-, or band-summations. With these approximations the accuracy of the results is greatly reduced by up to one order of magnitude or more.
The main difference between our calculations and what has been done in the past is that we do not use any such approximations but explicitly solve all involved integrations and summations. As a result, our calculations have been shown to agree with the experiment within less than a few ten percent uncertainty.
The shortcomings of the use of an Auger constant, C, and a power law, CN³, instead of calculating the underlying processes explicitly are demonstrated here.
For more details about this approach see Ref.[28]. For examples of the results of our approach see e.g. the description of the closed loop design or the examples.
NLCSTR provides Gain Databases (Tables) for standard III-V and II-VI material systems.
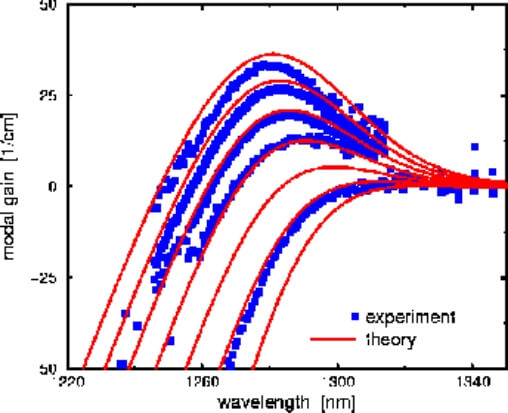
Our first principles microscopic approach avoids employing ad hoc model parameterization. The examples below illustrate key pitfalls encountered when designing an optimized and targeted semiconductor laser using the less rigorous approaches.
For more examples see the SimuLase manual and our various publications.
The calculation of carrier recombination’s due to Auger processes and the inverse process, carrier generation due to impact ionization, requires one to solve complex quantum-Boltzmann type scattering processes in the second Born-Markov approximation. The general equations that have to be solved have been known for decades. However, mostly due to numerical limitations, previous attempts to solve them have applied uncontrolled approximations for the involved (Coulomb) coupling matrix elements, spin-, k-, or band-summations. With these approximations the accuracy of the results is greatly reduced by up to one order of magnitude or more.
The above example demonstrates the errors arising from using a dephasing time or a line-broadening instead of calculating the underlying electron-electron and electron-phonon scattering processes explicitly. Even if experimental data is known and a decent fit to it can be found for one carrier density, the fit will fail for higher and lower densities. Also, spectral positions and the gain amplitude to carrier density relation will be significantly wrong. This approach requires the previous knowledge of the experimental result for any decent agreement. Thus, it has no predictive capabilities but relies on fitting.
These strong general shortcomings are inherent to all attempts using broadenings, no matter how ‘sophisticated’ they are. Although some methods (like ‘non-Markovian gain models’) avoid e.g. the non-physical absorption tail energetically below the gain that simple Lorentzian lineshape broadening produces, however this is merely cosmetics. The underlying microscopic scatterings are strongly dependent not only on the carrier density but also the temperature and spectral position. They introduce mixings of the complex microscopic polarizations that lead to spectral lineshape modifications, amplitude modifications, and energy renormalization that cannot be captured through broadenings of individual transitions.
The error in the density-amplitude relation would make any attempts to calculate input-output currents as demonstrated in Close Loop Design impossible. Since the loss currents scale more than linearly with the carrier density, errors in the threshold density of several tens of percent would lead to even bigger errors in the loss currents.
For shortcomings due to neglect of the conduction band nonparabolicity or the Coulomb induced intersubband coupling see e.g. Ref.[10].
Ratio between radiative carrier lifetimes as calculated with the semiconductor luminescence equations and those obtained when using the KMS-relation. Here, for the structure investigated in the example for the Closed Loop Design.
The above picture demonstrates the shortcomings of the Kubo-Martin-Schwinger (KMS) relation which calculates the spontaneous emission by a simple integral conversion of the gain/absorption spectra. The KMS relation is strictly valid only in the absence of any broadenings. However, the correct calculation of the absorption/gain requires the inclusion of the homogeneous broadening due to electron-electron and electron-phonon scattering.
The KMS-formula has a pole at the position of the chemical potential. If this is energetically in the low energy tail of the absorption it artificially enhances the spontaneous emission and, thus, leads to an underestimation of the radiative carrier lifetime which is given by the inverse of the integral over the spontaneous emission. Thus, the KMS-results can be off by a factor of two or more.
This error becomes most dramatic when the chemical potential is just below the bandgap, i.e. for densities just below transparency. For higher densities the chemical potential is at the position of the transparency point where absorption/gain is zero. This prevents an artificial pole in the results. However, as shown in the example above, since the KMS neglects the excitonic correlations that are included in the luminescence equations, the results of the KMS are wrong there too and so are in general the line shapes calculated with KMS.
Loss currents due to radiative recombination, JSE, divided by the carrier density. Bold lines: as calculated with the semiconductor luminescence equations. Thin lines: using the power law, JSE=BN². Here, the coefficient, B, was derived by fitting the power law to the low density result of the microscopic calculation at N=10¹¹/cm². The open signs mark the threshold carrier densities. Here for the GaInNAs/GaAs-structure investigated in the examples.
An often used, even simpler approach to calculating the carrier lifetimes due to spontaneous emission than using KMS is to use a power law, JSE=BN², to describe them. This power law holds approximately in the limit of very low carrier densities where the carrier distributions can be described by Boltzmann distributions.
However, it fails for densities where phase space filling becomes significant, i.e. near transparency and above. Even if as in the example above the exact value for B is known from the low density result, the results of the power law are off by about a factor of two near threshold and the error can easily reach one order of magnitude.
It can be shown analytically that for very high densities the density dependence of the radiative losses changes from quadratically to only linear. This can be seen in the picture above where JSE/N as calculated microscopically approaches a constant value for high densities.
For more details see e.g. Refs.[28] and [29].
Loss currents due to Auger recombination processes, Jaug, divided by the square of the carrier density. Bold lines: calculated microscopically. Thin lines: using the power law, Jaug=CN³. Here, the coefficient, C, was derived by fitting the power law to the low density result of the microscopic calculation at N=10¹¹cm². The open signs mark the threshold carrier densities. Left: for the GaInNAs/GaAs-structure investigated in the examples. Right: for the InGaAsP/InP-structure operating at 1.5µm.
Auger recombination losses are often described using a simple power law for the loss current, Jaug=CN³. Using some rough approximations, this density dependence can be shown analytically to be correct for low densities where the carrier distributions can be described by Maxwell-Boltzmann distributions. However, for in the regime important for laser operation, i.e. near transparency and above, the density dependence becomes less than cubic. As shown for two examples in the picture above, here, the density dependence can become only quadratically (which would yield horizontal lines in the way the data is plotted in the picture) or even less.
Ratios between microscopically calculated loss currents and loss currents when using power laws with the coefficients B and C fitted to the microscopic results at low densities. Red: loss currents due to spontaneous emission. Black: loss currents dur to Auger processes. Results for the InGaAsP/InP-structure operating at 1.5µm.
The above picture demonstrates, as in the two previous pictures, the shortcomings of the power laws, JSE=BN² and Jaug=CN³. Near threshold the power laws are off by a factor of three. For higher densities the error can easily reach one order of magnitude or more.
For more details see e.g. Refs.[28] and [29].
